Paper Review 3: Network in Network
Motivation
- CNN is capable when concept is “linearly separable”
- But concepts are non-linear → Need nonlinear function!
- Replace Linear Model with Non-linear function → micro network structure (Network in Network)
Network in Network
Radial Basis Network or Multilayer perceptron are capable of capturing latent concepts (Universal function approximator)
Why used multilayer perceptron for non-linear function? (rather than Radial basis Network?)
- Compatible with the structure of CNN, which uses back-propagation
- Can be deep-model itself, which is consistent with feature re-use
Structure
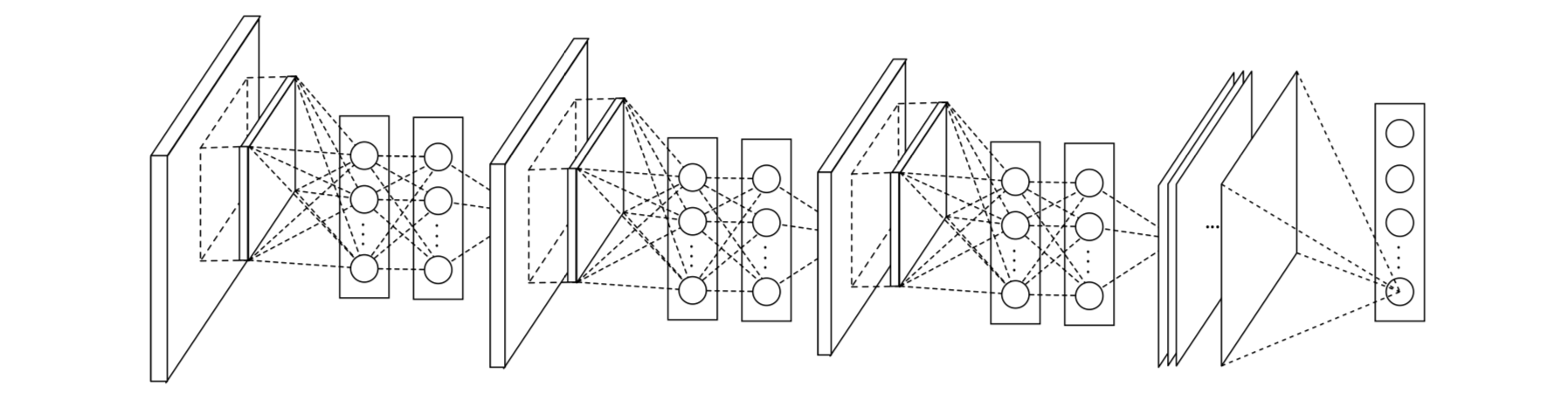
Features
- Equivalent to cascaded cross channel parametric pooling on CNN
- Equivalent to 1x1 conv kernel
Universal Function Approximator란?
- 어떤 연속 함수라도 Hidden Layer 여러 개를 통해 근사 가능!
- 따라서, Hidden Layer 여러개 쌓으면 Function Approximate 가능함
https://dlaiml.tistory.com/entry/Universal-Approximation-Theorem
참고) Universal Approximation Theorem → 이론적으로 하나의 hidden layer와 비선형의 연속적인 활성화 함수를 사용하면 어떠한 연속함수라도 근사가 가능하다는 이론
Comparison to Max Pooling Layers
- Maxpool → capable of modeling any “convex” function
- But features are not always on convex function! → Need Universal function approximator
Global Avg Pooling
Why global avg pooling?
- More native to CNN Structure by enforcing correspondences between feature maps and categories
- No parameter to optimize → avoid overfitting (FC layer is prone to overfitting)
- Sums out spatial information
Visualization of NIN
