1. Summary

Reduce computational cost with linear bottleneck layer which preserves manifold of interests with lower dimensions and serves as a linear transformation

2. Intuitions

2-1. Depthwise Separable Convolutions

Same as MobileNetV1

2-2. Linear Bottlenecks

Manifold of interest

  • Set of layer activations forms “manifold of interest” (information that encodes values lie in some manifold) ⇒ Embeddable into low dimensional subspace
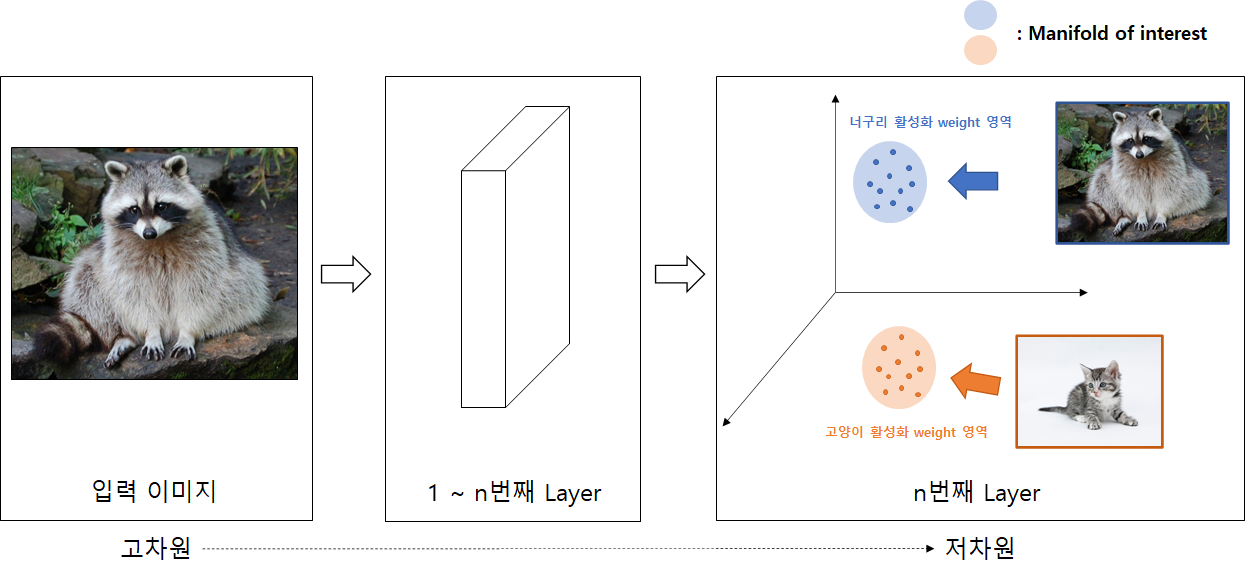
  • FYI) If manifold of interest spans entire space, width multiplier (MobileNetV1) allows to reduce the dimensionality
    • But because we have non-linear per coordinate transformations (ReLU), we cannot do this

Properties of ReLU

  1. If manifold of interest remains non-zero volume after ReLU transformation (= when input > 0), it corresponds to linear transformation
  2. ReLU is capable of preserving information about input manifold but only if input manifold lies in low-dimensional subspace of input space
    • Information of low dimension could be preserved when we use lots of channels (because even though ReLU collapses information, it might still be preserved in the other channels)

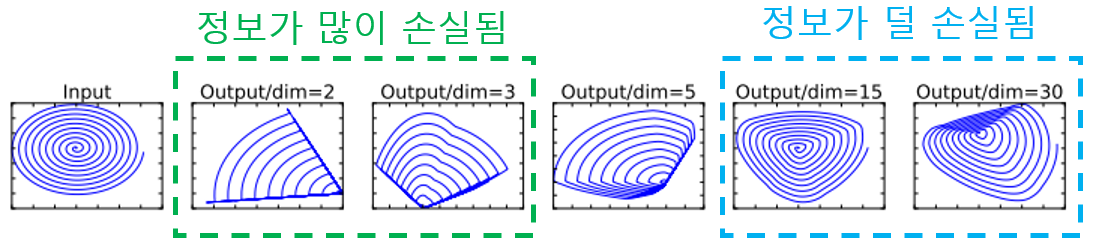
Intuitions by properties of ReLU

  • Assuming manifold of interest is low-dimensional → Can capture manifold of interest by inserting “linear bottleneck layers” into conv layer - Bottleneck is linear → information is preserved because it it linear transformation - Bottleneck is non-linear → Preserve information with many channels

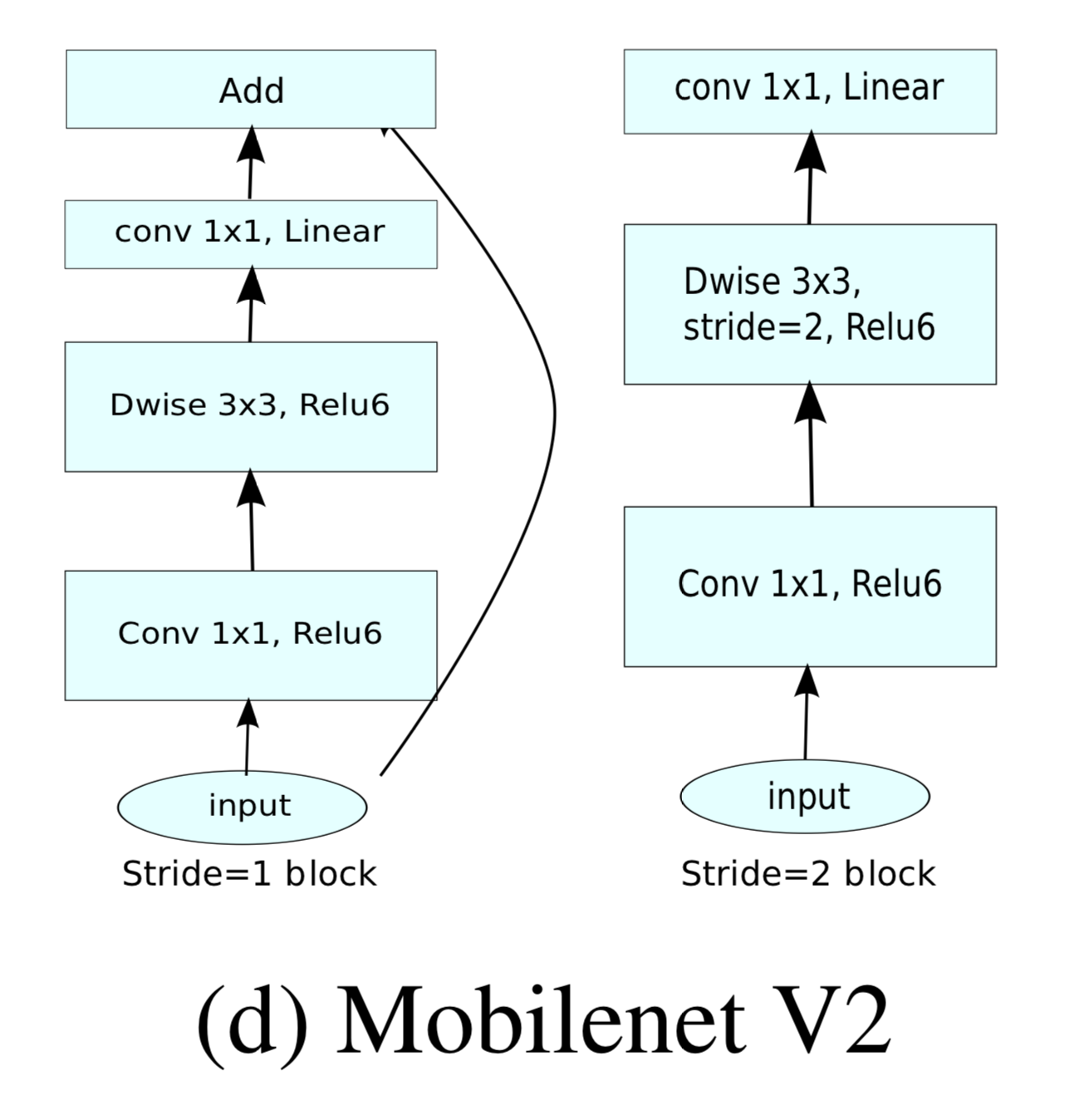
2-3. Inverted Residuals

Because information is already embedded in the bottleneck layer, there is no need to do residual connection between high-dimensions

  • Use shortcuts directly between the bottlenecks to reduce computational costs

\[Cost = h_i·w_i·d_i(k^2+d_i)\]

\[Cost = h·w·d'·t(d'+k^2+d'')\]

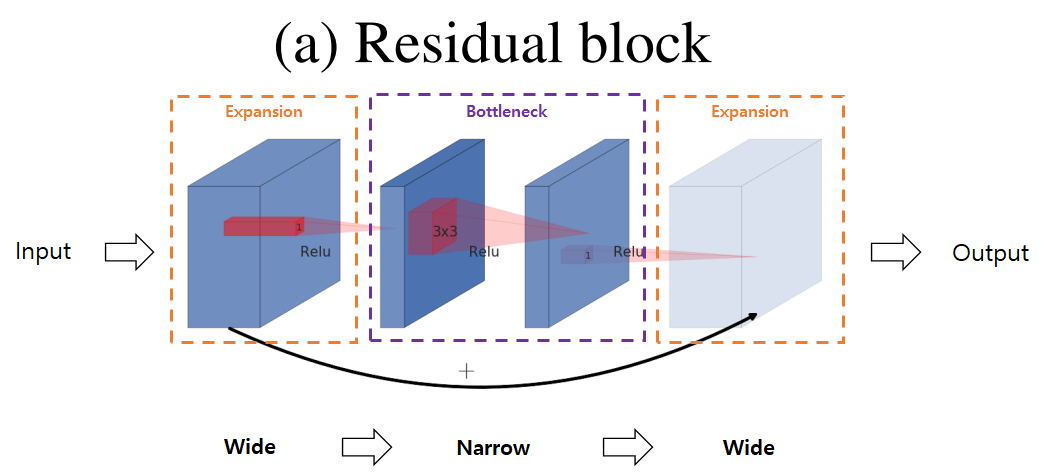
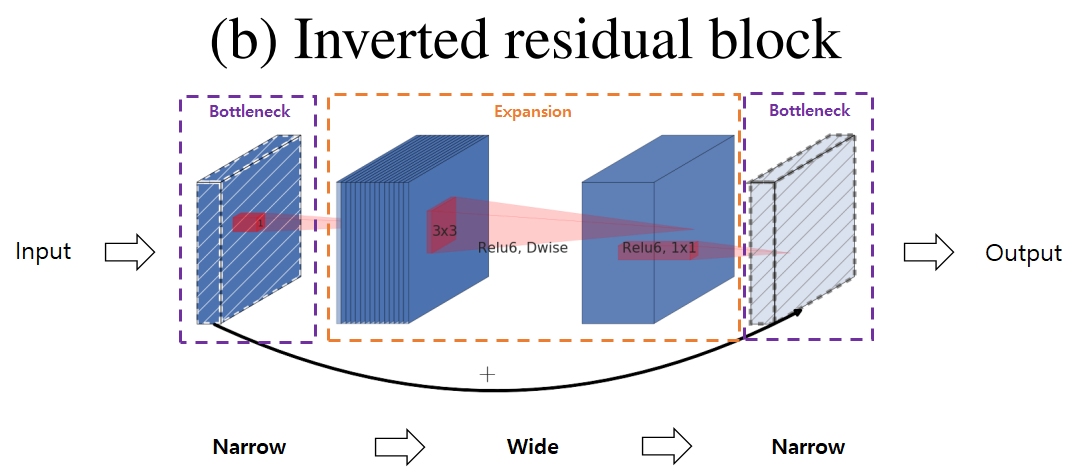
Because dimension is smaller, computational cost is reduced

3. MobileNetV2 Architecture

4. Ablation study

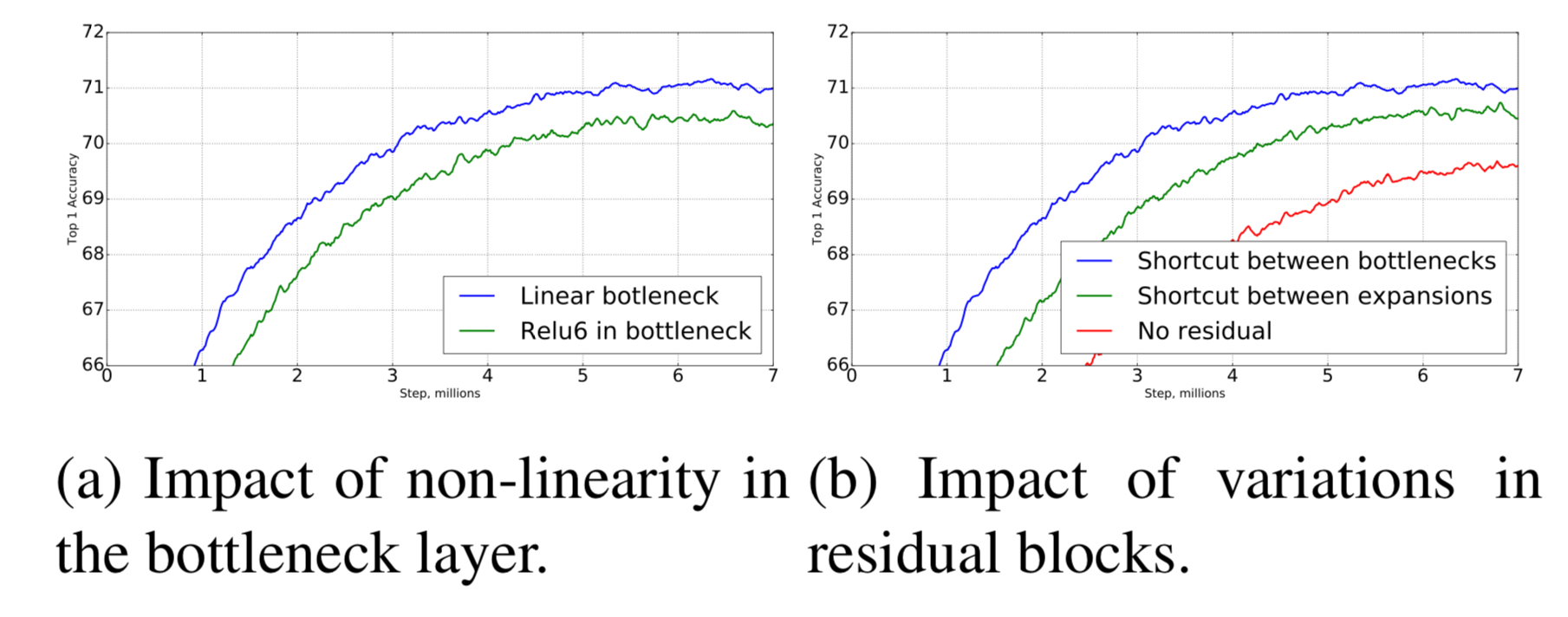
4-1. Inverted residual connections

4-2. Importance of linear bottlenecks

  • With CIFAR dataset, “linear” bottleneck outperforms non-linear bottleneck