1. Summary

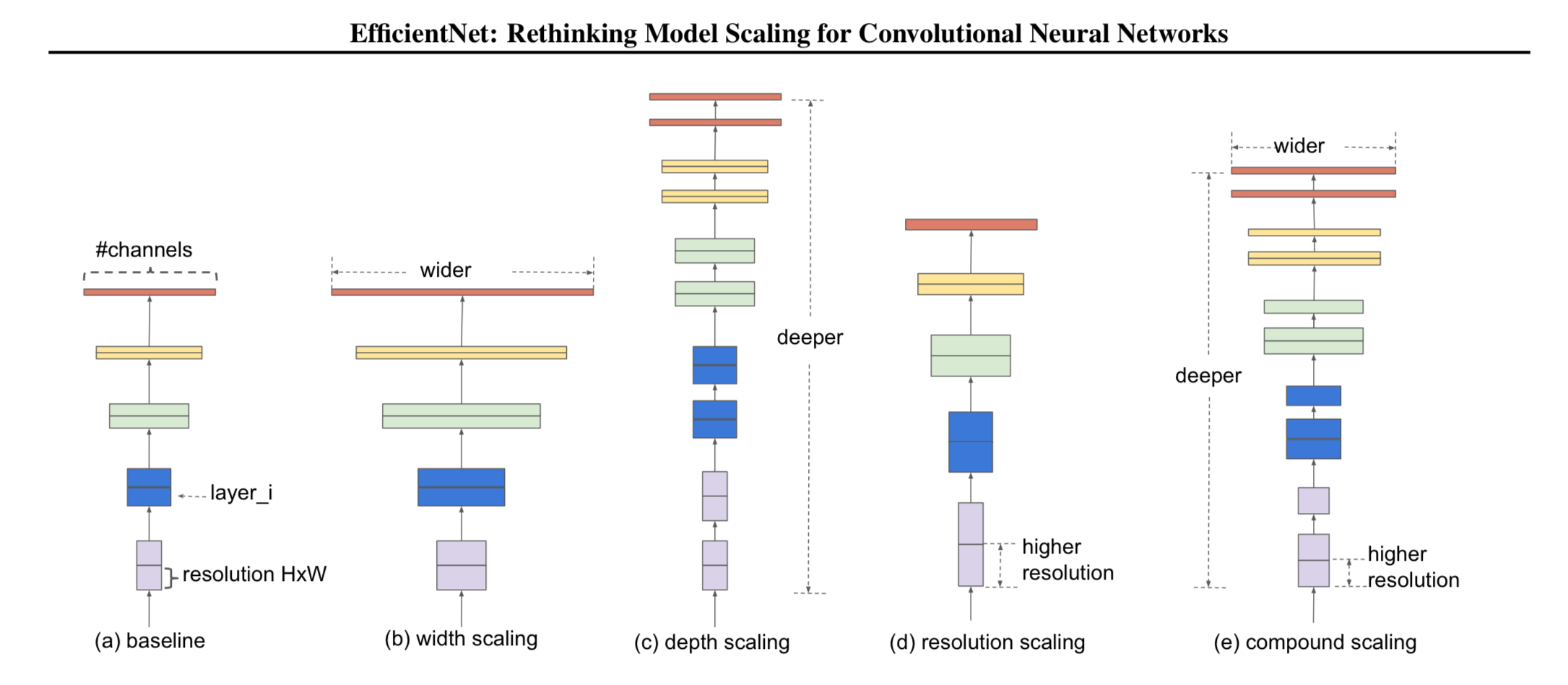
This paper propose compound coefficient which uniformly scales all dimensions of depth/width/resolution for better performance

ɑ, β, 𝛾 are constants determined by a small grid search

\[depth: d = ɑ^ϕ\\ width:w=β^ϕ\\ resolution:r=𝛾^ϕ\] \[ɑ·β·𝛾≈2\\ ɑ≥1, β≥1, 𝛾≥1\]

Compund scaling method

  • STEP 1 : fix ϕ = 1, perform small grid search of ɑ, β, 𝛾.
  • STEP 2 : fix ɑ, β, 𝛾 then scale up network with different ϕ

2. Problem Formulation

2-1. Define ConvNet (N)

\[N = \bigodot_{i=1...s}F_i^{L_i}(X_{<H_i\ ,\ W_i\ ,\ C_i>})\]
  • F_i^{L_i} denotes layer F_i repeated L_i times in stage i.

  • FYI) N is represented by a list of composed layers

    \[N=F_k⊙...\ ⊙F_2⊙F_1(X_1) = \bigodot_{i=1...k}F_j(X_1)\]

2-2. Formulate Optimization Problem

\[\max_{d,w,r} \ Accuracy(N(d, w, r))\]

When

\[N(d,w,r)=\bigodot_{i=1..s}\hat{F}^{d·\hat{L}_i}(X_{r·\hat{H}_i\ ,\ r·\hat{W}_i \ ,\ w·\hat{C}_i})\\ Memory(N) ≤ target\_memory\\ FLOPS(N) ≤ target\_flops\]

3. Observations and Intuitions

  1. Scaling up any dimension of network width, depth, or resolution improves accuracy but accuracy gain diminishes for bigger models
  2. Different scaling dimensions are not independent → it is critical to balance all dimensions of network width, depth and resolution
    • EX) Higher resolution
      • → should increase depth to capture more features
      • → should increase width to capture more patterns