Partition with Grids and predict bounding boxes per Grid

How to implement Grids? → ConvNet!

1. Architecture

  1. Divides input image into S x S grid

  2. Each grid cell predicts B bounding boxes and confidence scores for those boxes

    \[Confidence=P_r(Object)*IOU^{truch}_{pred}\]
    • No object → 0 Else → we want it to equal to IOU between predicted box and ground truth
    • Bounding box consists of 5 predictions: (x, y, w, h, confidence)

  3. Each grid cell predicts C conditional class probabilities

    \[P_r(Class_i|Object)\]
    • Only predicts 1 set of class probabilities per grid cell, regardless of the number of boxes B

  4. At test time, multiply conditional class probabilities and individual box confidence predictions, which gives class-specific confidence scores for each box

    \[P_r(Class_i|Object)*P_r(Object)*IOU^{truth}_{pred}=P_r(Class_i)*IOU^{truth}_{pred}\]

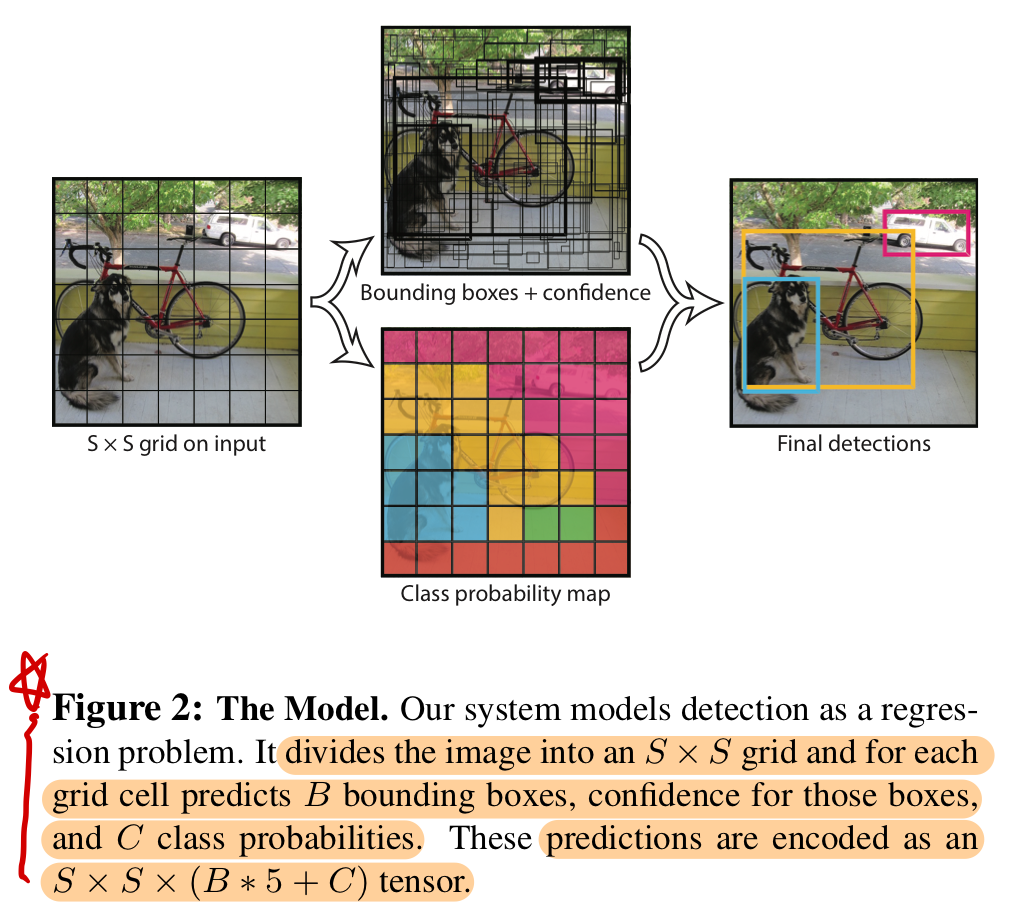
Each grid consists of B bounding boxes(Confidence, x, y, h, w) and C class probabilities

\[(C_{b_1}, b_{1x}, b_{1y}, b_{1h}, b_{1w}, C_{b_2}, b_{2x}, b_{2y}, b_{2h}, b_{2w}, ...\ , c_1, c_2, ... \ ,c_n)\]

Implementation

2. Loss Function

Meaning of λ

  • Sum-squared error makes localization error equal to classification error → Not ideal
  • Many grid cells doesn’t contain any objects → Makes confidence scores towards zero
  • Remedy this with λ_coord and λ_noobj to increase loss from bounding box predictions and decrease loss from confidence predictions that don’t have objects.

Meaning of 1

\[\mathbf{1}_{i}^{obj} = if \ object \ appears\ in\ cell\ i \\ \mathbf{1}_{ij}^{obj} = jth\ bounding\ box\ predictor\ in\ cell\ i\ is\ responsible\ for\ prediction\]

Characteristics

  • Only penalizes classification error if an object is present in that grid cell
  • Only penalizes bounding box coordinate error if that predictor is responsible for the ground truth box

3. Advantages of YOLO

  1. Extremly fast because it is just a regression problem and doesn’t need complex pipeline
  2. Reasons globally about the image when making predictions
  3. Learns generalizable representations of objects

4. Limitations of YOLO

  1. Can predict limited number of nearby objects because each grid cell only predicts B boxes.
  2. Struggles to generalize to objects in new or unusual aspect ratios or configurations
  3. Loss function treats errors the same in small bounding boxes vs large bounding boxes
    • Small error in a large box is generally benign but a small error in a small box has a much greater effect on IOU