Summary
This paper analyzes LSTM, GRU and traditional tanh units to show
- LSTM and GRU are superior to traditional tanh units
- GRU is comparable to LSTM
Background Study: RNN
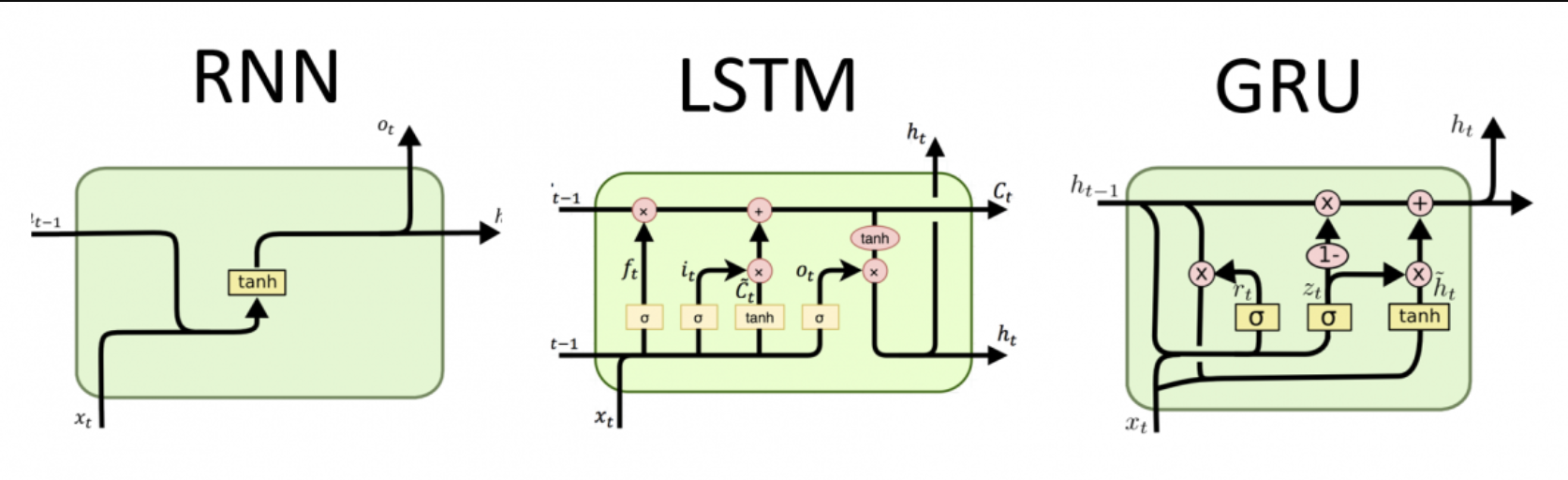
RNN
-
RNN is able to handle a variable-length sequence input by having a recurrent hidden state whose activation at each time is dependent on that of the previous time
\[\text{sequence }x=(x_1,x_2,...,x_r) \\ \mathbf{h}_t = \begin{cases} 0, & t = 0 \\ \phi(\mathbf{h}_{t-1}, \mathbf{x}_t), & \text{otherwise}\end{cases}\] -
Update of the hidden state is implemented as below
\[h_t=g(Wx_t+Uh_{t-1})\] -
We model each conditional probability distribution with
\[p(x_t|x_1,...,x_{t-1})=g(h_t)\]
Limitation of RNN
- Unable to capture long-term dependencies because of the vanishing/exploding gradient problem
Solution
- Devise a better learning algorithm than a simple stochastic gradient descent
- Design a more sophisticated activation function (LSTM, GRU)
LSTM (Long-Short-Term Memory)
Notations
\[h_t^j:\text{j-th LSTM unit's activation at time t}\\ o_t^j:\text{output gate}\\ f_t^j:\text{forget gate}\\ i_t^j:\text{input gate}\\ c_t^j:\text{memory}\\ \tilde{c}^j_t:\text{newly computed memory}\\\]Unlike traditional RNN which computes weighted sum and nonlinear function, LSTM maintains memory c
\[h_t^j=o_t^j\tanh(c_t^j)\]Output gate modulates the mount of memory content exposure
\[o_t^j=σ(W_ox_t+U_oh_{t-1}+V_oc_t)^j\]Memory cell c is updated by partially forgetting the existing memory and adding a new memory content tilde(c)
\[c_t^j=f_t^jc^j_{t-1}+i^j_t\tilde{c}^j_t\]New memory content tilde(c) is
\[\tilde{c}^j_t=\tanh(W_cx_t+U_ch_{t-1})^j\]Forgetting memory is modulated by forget gate f / Degree of adding new memory is modulated by input gate i
\[f_t^j=σ(W_fx_t+U_fh_{t-1}+V_fc_{t-1})^j\\ i_t^j=σ(W_ix_t+U_ih_{t-1}+V_ic_{t-1})^j\]GRU (Gated Recurrent Unit)
Notations
\[h_t^j:\text{activation}\\ \tilde{h}_t^j:\text{candidate activation}\\ z_t^j:\text{update gate}\\ r_t^j:\text{reset gate}\\ \odot :\text{element-wise multiplication}\]Similar to LSTM but without having separate forget gate and output gate. GRU exposes whole state each time.
\[h_t^j=(1-z_t^j)h^j_{t-1}+z_t^j\tilde{h}^j_t\]Update gate z decides how much to update content.
\[z_t^j=σ(W_zx_t+U_zh_{t-1})^j\]candidate activation function tilde(h) is
\[\tilde{h}^j_t=\tanh(Wx_t+U(r_t\odot h_{t-1}))^j\]Reset gate r make the unit forget previously computed state
\[r_t^j=σ(W_rx_t+U_rh_{t-1})^j\]Experiments
Evaluate LSTM, GRU, tanh units with the task of polyphonic music modeling and speech signal modeling.
What sequence models aim is to learn a probability distribution over sequences, which is achieved by maximizing the log-likelihood of a model given a set of training sequences. (θ below is a set of model parameters)
\[\max_{\theta} \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \log p \left( x_t^n \mid x_1^n, \dots, x_{t-1}^n ; \theta \right)\]Results
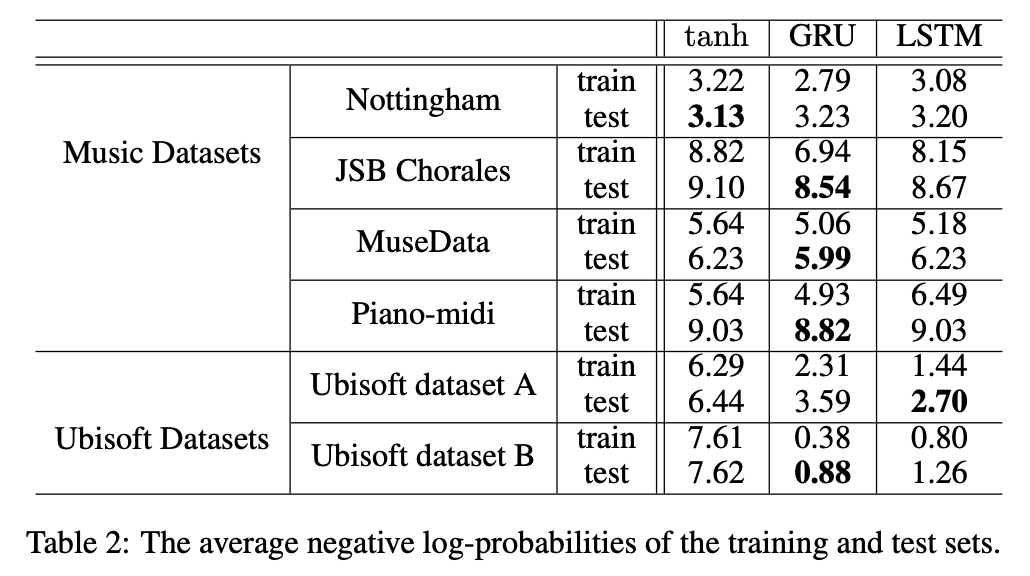
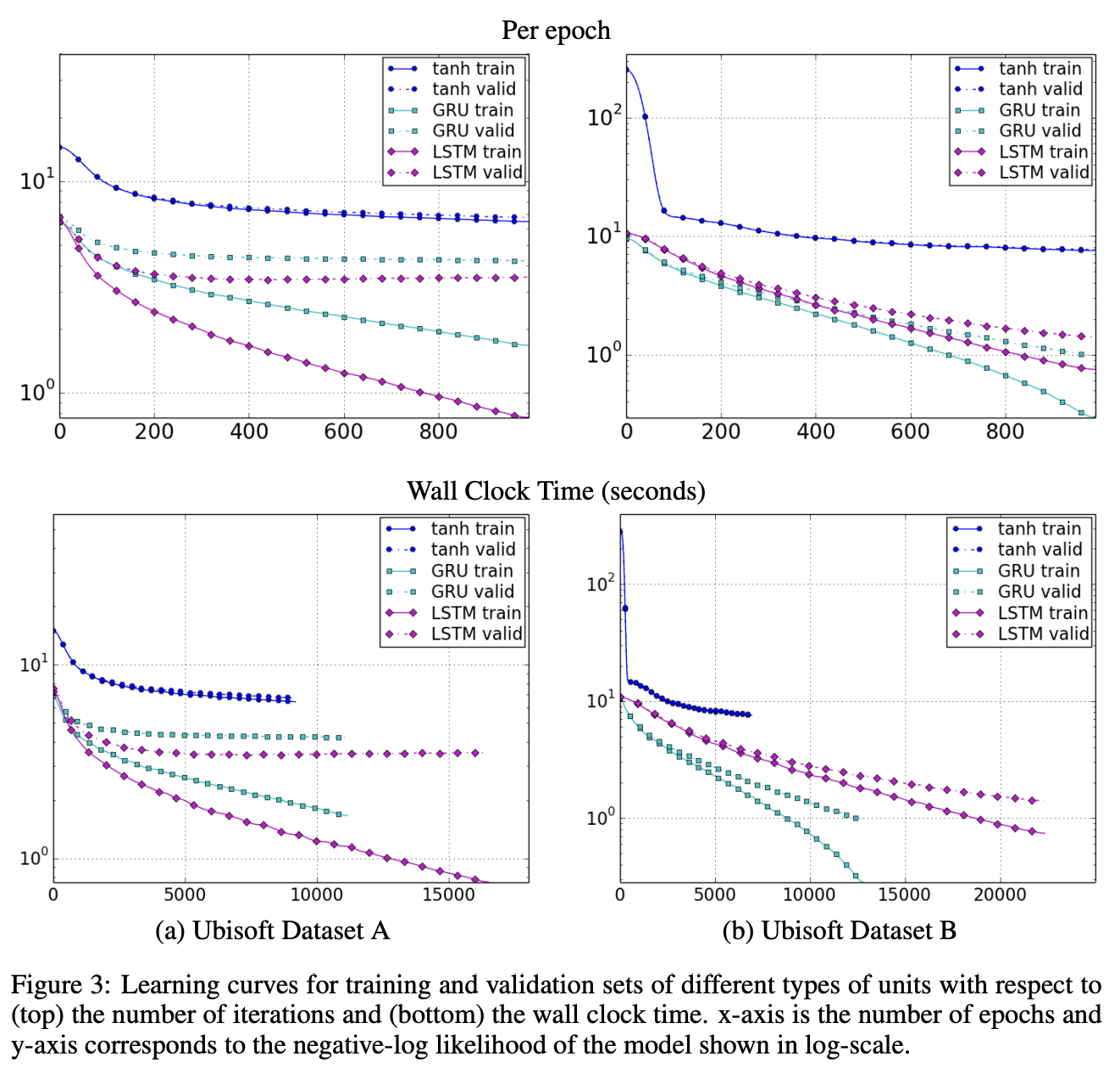
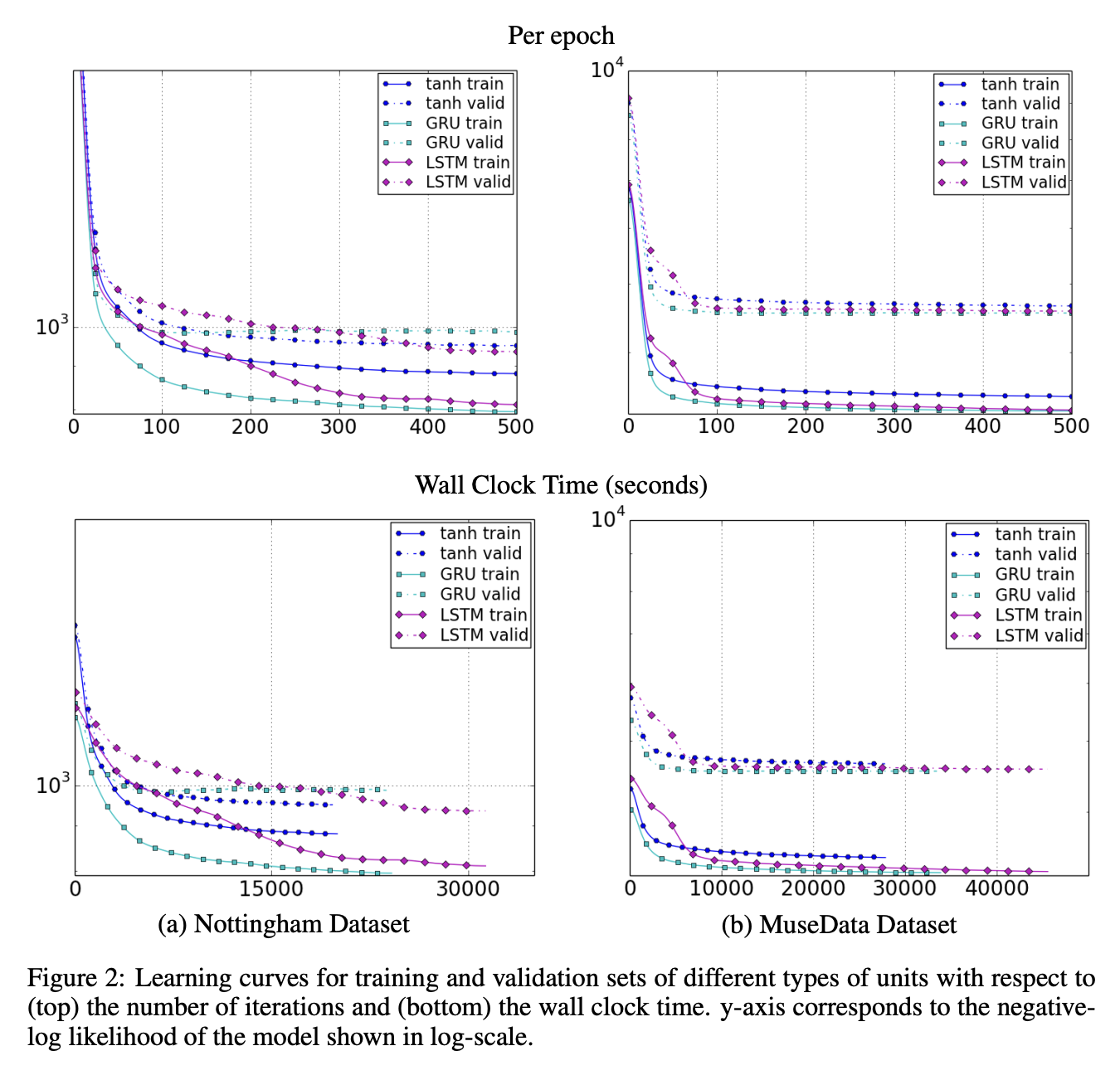
Results indicate the advantages of the gating units over the more traditional recurrent units. Convergence is often faster, and the final solutions tend to be better.
However, results are not conclusive in comparing the LSTM and the GRU, which suggests that the choice of the type of gated recurrent unit may depend heavily on the dataset and corresponding task.
-
Log probability: GRU, LSTM outperformed traditional tanh units.
-
Learning curves: Both GRU and LSTM are faster than tanh units. But superiority cannot be chosen between GRU and LSTM with these experiments.