1. SNE (Stochastic Neighbor Embedding)
1-1. Intro
- Computes similarity by converting Euclidean distances into conditional probabilities.
- Using Gaussian distribution centered at x(i), p(j | i) means probability that x(i) would pick x(j) as its neighbor
- Nearby datapoint → p(j | i) ↑
- Far datapoint → p(j | i) ↓
1-2. SNE process
-
In high dimension, probability is computed with Gaussian distribution
\[p_{j|i} = \frac{\exp \left( -\|x_i - x_j\|^2/2\sigma_i^2 \right)} {\sum_{k \neq i} \exp \left( -\|x_i - x_k\|^2/2\sigma_i^2 \right)}\] -
In low dimension, probability is computed with Gaussian distribution
\[q_{j|i} = \frac{\exp \left( -\|y_i - y_j\|^2 \right)}{\sum_{k \neq i} \exp \left( -\|y_i - y_k\|^2 \right)}\] -
To make q (low dimension) have similar distribution to p (high dimension), learn to minimize KL divergence
\[Cost = \sum_{i} KL(P_i \parallel Q_i) = \sum_{i} \sum_{j} p_{j|i} \log \frac{p_{j|i}}{q_{j|i}}\]
2. t-SNE (t-distributed SNE)
2-1. Problems of SNE
- Conditional probability is asymmetric → Not easy to optimize
- Crowding Problem → Points are gathered together in low dimension
2-2. Symmetric SNE
In high dimensions, symmetrize conditional probability by
\[p_{ij}=\frac{p_{j|i}+p_{i|j}}{2n}\]This improves performance because it converges at any directions!
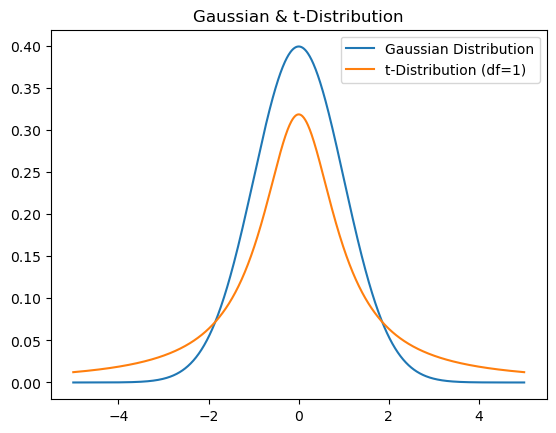
2-3. Using t-distribution on low dimension
In low dimensions, use t-distribution to make points become far away.
\[q_{ij} = \frac{(1 + \|y_i - y_j\|^2)^{-1}}{\sum_{k \neq l} (1 + \|y_k - y_l\|^2)^{-1}}\]The reason why it can make it far is because it has heavy-tailed characteristic.
2-4. t-SNE process
-
In high dimension, probability is computed with Gaussian distribution
\[p_{j|i} = \frac{\exp \left( -\|x_i - x_j\|^2/2\sigma_i^2 \right)} {\sum_{k \neq i} \exp \left( -\|x_i - x_k\|^2/2\sigma_i^2 \right)}\] \[p_{ij}=\frac{p_{j|i}+p_{i|j}}{2n}\] -
In low dimension, probability is computed with t-distribution (freedom = 1)
\[q_{ij} = \frac{(1 + \|y_i - y_j\|^2)^{-1}}{\sum_{k \neq l} (1 + \|y_k - y_l\|^2)^{-1}}\] -
To make q (low dimension) have similar distribution to p (high dimension), learn to minimize KL divergence using joint probability distributions P and Q.
\[C = KL(P \parallel Q) = \sum_{i} \sum_{j} p_{ij} \log \frac{p_{ij}}{q_{ij}}\]