Summary
Introduced debiasing word embedding algorithms using the properties below
- Gender bias is captured by a direction in the word embedding
- Gender neutral words are linearly separable from gender definition words
It can be performed by 1. Identify gender subspace and 2. debiasing
Geometry of Gender and Bias
Gender subspace
We can measure gender direction $g \in \mathbb{R}^d$ by aggregating across multiple paired comparisons
\[\overrightarrow{\text{grandmother}} - \overrightarrow{\text{grandfather}} = \overrightarrow{\text{gal}} - \overrightarrow{\text{guy}} = g\]Direct Bias
Association between a gender neutral word and a clear gender pair.
Given gender neutral words $N$ and gender direction $g$
\[\text{DirectBias}_c = \frac{1}{|N|} \sum_{w \in N} |\cos(\vec{w}, g)|^c\]Indirect Bias
Association between gender neutral words that are clearly arising from gender.
Given $w = w_g + w_{\perp}$ where $w_g=(w \cdot g)g$ ,
\[\beta(w,v)=(w\cdot v\ - \frac{w_{\perp} \cdot v_{\perp}}{\|w_{\perp}\|_2\|v_{\perp}\|_2})/w \cdot v\]- This measures the degree of gender impact! (measures how much the inner product changes after removing the gender subspace)
Debiasing algorithms
Subspace $B$ is defined by $k$ orthogonal unit vectors $B={b_1,…,b_k} \subset \mathbb{R}^d$
Projection of a vector $v$ onto $B$ is denoted as
\[v_B=\sum^k_{j=1}(v \cdot b_j)b_j\]-
Identify Gender Subspace
Calculate bias direction by using
Inputs: word sets $W$, Defining Sets(pair of words that varies by gender) $D_1,…D_N \sub W$, embedding ${\vec{w}\in \mathbb{R}^d}_{w\in W}$
\[\mu_i := \sum_{w \in D_i} \vec{w}/|D_i|\]Let the bias subspace $B$ be the first $k$ rows of $\text{SVD}(C)$ where
\[C := \sum^n_{i=1}\sum_{w\in D_i}(\vec{w}-\mu_i)^T(\vec{w}-\mu_i)/|D_i|\]What are they?
$\mu$ is average of the defining sets and then, $C$ is a covariance matrix that captures the variance of the word vectors within each defining set. → $C$ captures how words in gender-related pairs vary from their mean.
Trivial SVD sorts the eigenvalues in descending order. So, after performing SVD(C), we can get more important values (=which has higher covariance) by getting first k rows of it
-
Hard de-biasing (neutralize & equalize)
Inputs: words to neutralize $N \subseteq W$, family of equality sets $\mathcal{E} = { E_1, E_2, \ldots, E_m }$
-
Neutralize ensures that gender neutral words are zero in the gender subspace
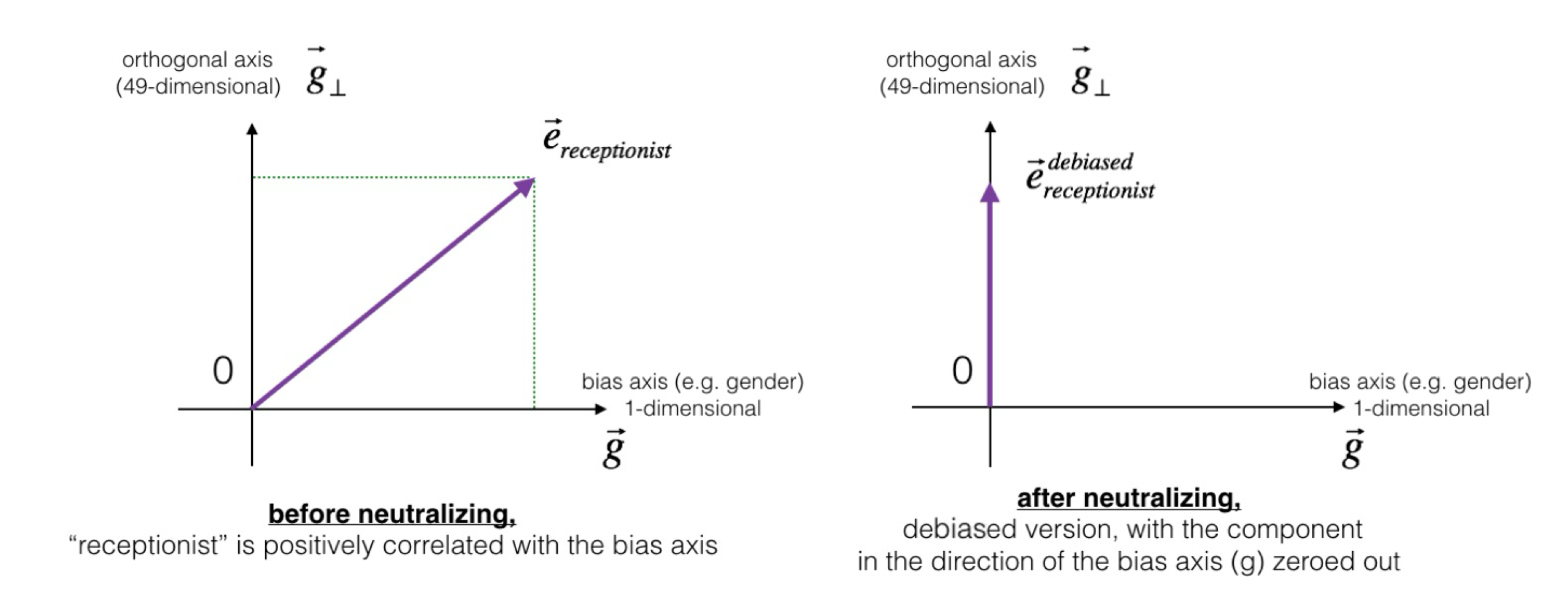
$\vec{w}_B$ is a projection of a word vector $\vec{w}$ onto the subspace $B$.
-
Equalize equalizes sets of words outside the subspace by enforcing any neutral words to be equidistant to all words in each equality set
\[\mu := \sum_{w \in E} \frac{w}{|E|} \\ \nu := \mu - \mu_B \\ \text{For each } w \in E, \quad \vec{w} := \nu + \sqrt{1 - \|\nu\|^2} \frac{\vec{w}_B - \mu_B}{\|\vec{w}_B - \mu_B\|}\]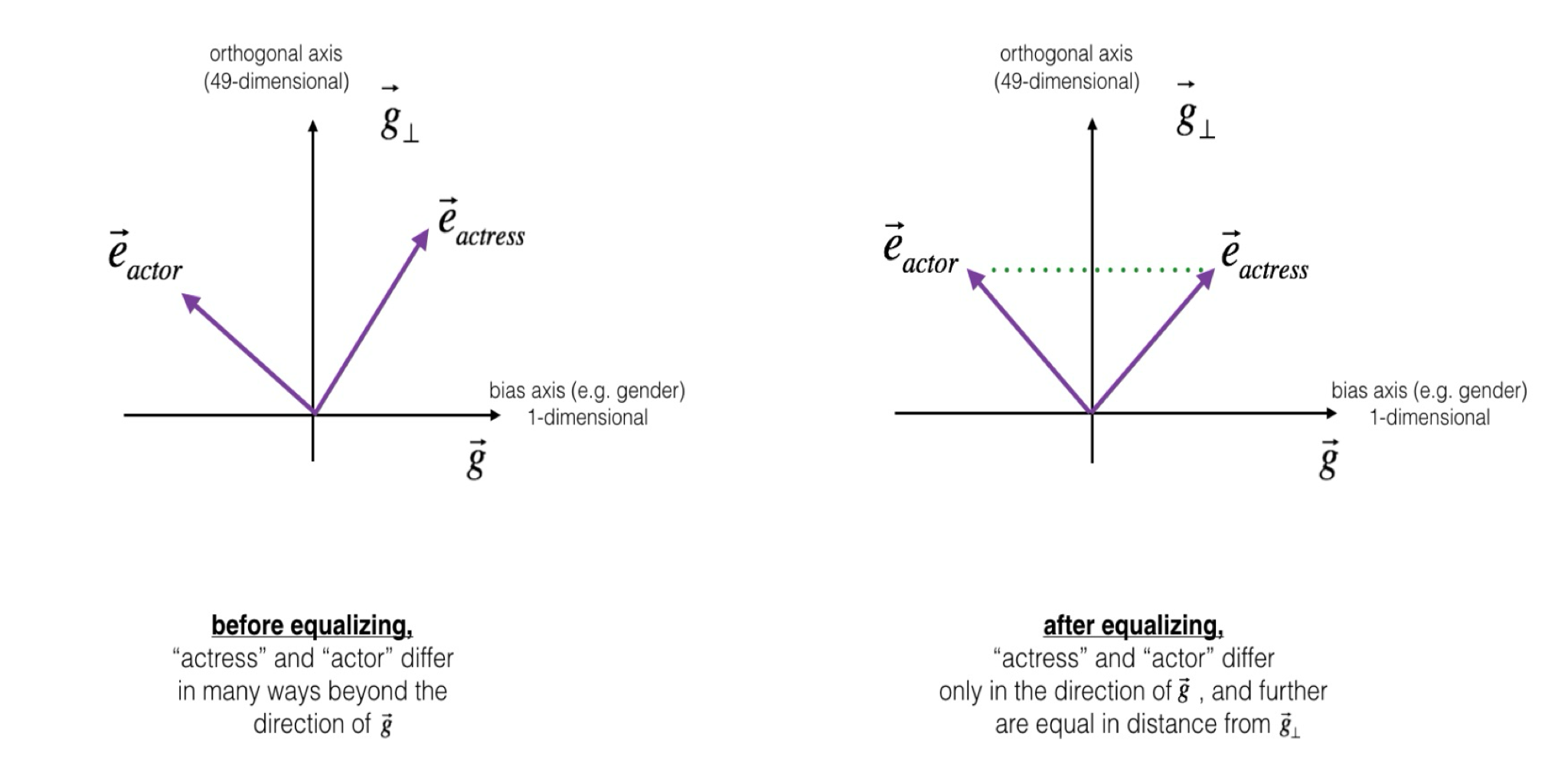
First, calculate the average word direction $\mu$ and then calculate the “middle vector” $\nu$ by subtracting the projection onto the subspace $\mu_B$
Then, make $\vec{w}$ to be equidistant from the middle vector!
-